《模型思维》阅读指引

1.正态分布(Normal Distribution)

正态：正常状态，按照英文normal的理解就是正常的。正态，正常状态的

分布：按照字面理解就是分散到各处、散布

正态分布：正常状态的分布、散布

1.1 函数（Function）

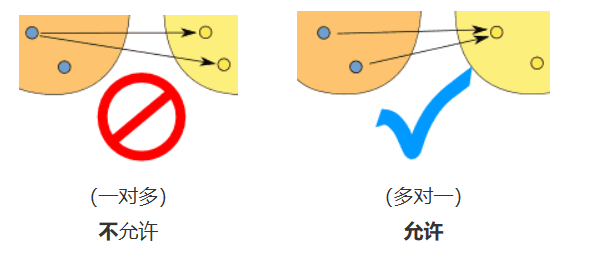
函数：函数把一个集合里的每一个元素联系到另一个集合里（也可以是同一个集合）一个独一的值

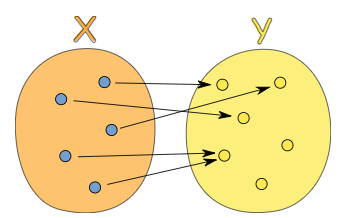
两个重点

每一个元素的意思是X里的所有元素都与Y里的某一个元素有关系，但Y里的一些元素可能和X里的元素没有关系
独一的值的意思是函数是单值的。一个输入值不能有多于一个输出值，所以f(x)=7或9是不允许的

函数是从定义域到值域的一个映射

1.2 随机变量（Random variable）

随机：形容一件事的结果有一系列可能性

变量：变化的量，可以改变的量

随机变量：注意这里的英文Random variable，其中Random是形容词，variable是名词，也就是说随机变量可以说成随机的变量，随机变量是一个随机试验结果的可能数值

随机变量通常用大写字母表示，像X或Y，区别于代数变量x或y

随机变量有个数值集合，变量可以随机地取集合里的任何的值

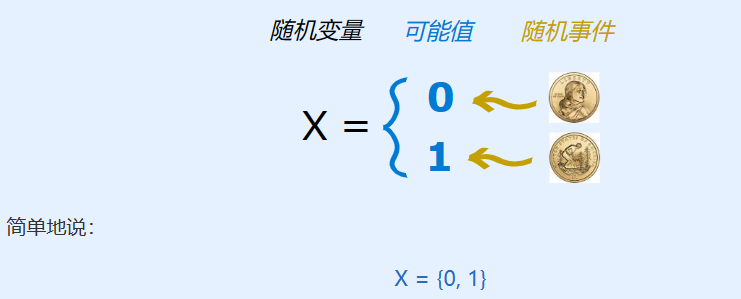
比如抛硬币的结果可以是正面或反面

这就是一个随机变量，因为试验的结果具有正面和反面的可能性，所以是随机变量，我们令这个随机变量为X，那么

X={正面，反面}

但是在数学研究中，我们习惯于用数字来高度概括、抽象我们研究的内容，所以我们令：

正面=0，反面=1，所以随机变量可以改写成：

X={0，1}

通过上一小节的函数的定义：函数是从定义域到值域的一个映射我们知道：

正面————>0

反面————>1

所以随机变量其实就是一个函数X=X(w)

总结：
1. 随机变量是随机实验结果的可能数值的集合
2. 可能数值的集合是它的样本空间
3. 随机变量使用大写字母来表示，例如X或Y
4. 随机变量可以是离散或连续的数据

1.3 离散和连续（Discrete Data and Continuous Date）

离散：离散数据是数出来的
连续：连续的数据是测量出来的

举例：

1.离散数据只能是某些既定的值

班上学生的人数（不能有半个学生）
掷骰子的结果（2，3，4，5，6，7，8，9，10，11，12）

2.连续数据可以是一个范围里任何的值

身高：可以是任何的值（人类身高范围里）
体重：狗的体重
长度：叶子的长度
……

连续数据都是需要测量的，而离散数据都是数出来的。这就是连续数据和离散数据的根本区别

1.4 试验和样本空间（Experiment and Sample Space）

试验：结果不肯定的行动，比如抛硬币、掷骰子、调查人们对薄饼的喜好都是试验的例子

样本空间：试验所有的可能结果，比如从一副扑克牌选一张牌（不包括小丑牌）

样本空间是52张牌：{红心A，红心2……等等}

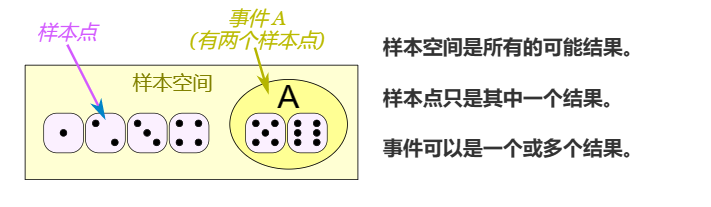
样本点：一个可能结果，比如一副扑克牌

梅花5是个样本点

红心国王是个样本点

国王不是样本点，因为有4个国王

事件：试验的一个成果

抛硬币得到反面是个事件

掷骰子拿到5是个事件

从一副扑克牌选一张国王是个事件

掷骰子得到偶数（2，4，6）也是个事件

事件可以包含一个或多个单项结果：

1.5 平均（ Mean）

1.5.1 算术平均数（ Arithmetic Mean）

算术平均数：把所有的数加起来，然后除以数的数目。也就是和除以量

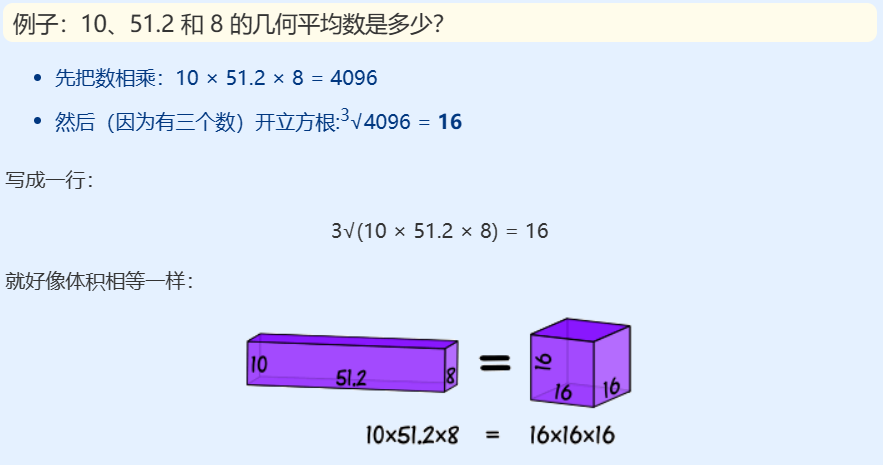
1.5.2 几何平均数（ Geometric Mean）

几何平均数：n个数， $a_1$ 到 $a_n$ 把所有数相乘，然后开n次方根

$\sqrt[n]{a_1\times a_2\times a_3\times ….\times a_n}$

1.5.3 加权平均数（Weighted Mean）

加权平均数：某些数值占较高比重的平均值，加权平均值的计算公式

$加权平均值 = \frac{\sum wx}{\sum w}$

其中， $w$ 代表权数， $x$ 代表对应的数值，把结果加起来，然后除以权数 $w$

1.6 方差和标准差（Standard Deviation and Variance）

1.6.1 方差

方差：离平均的平方距离的平均

计算方差的步骤：

求数值的平均
从每一个数值减去平均，然后求差的平方
求结果的平均

举例：

给定5个数字：600，470，170，430，300

1.第一步求平均：

$平均=\frac {600+470+170+430+300}{5}=\frac{1970}{5}=394$

2.第二步每个数值减去平均，然后求差的平方

$|600-394|^2,|470-394|^2,|170-394|^2,|430-394|^2,|300-394|^2$

分别是： $206^2,76^2,224^2,36^2,94^2$

3.求结果的平均

$方差=\frac{108520}{5}=21704$

1.6.2 标准差

标准差：标准差是方差的平方根

上例中标准差为

$\sigma = \sqrt{21704} = 147.32 =147$

1.7 期望（Expected Value）

期望：如果我们知道每个数值 $x$ 的概率，我们便可以计算 $x$ 的期望值（即加权平均值）

$\mu =\sum\limits_{i=1}\limits^n{} x_i·p_i$

其中 $x$ 代表数值， $p$ 代表数值对应的概率（注意下面的数字对应的概率并不是全部相等，比如数字6对应的概率为0.5）

1.7.1 离散随机分布的方差

在上面的例子中，每个数值都对应着一个概率，且概率是不相等的，它的方差通用公式为：

$Var(X) =\sum\limits_{i=1}\limits^n p_i·(x_i-\mu)^2 = \sum\limits_{i=1}\limits^n(p_i·x_i^2)-\mu^2$

此处 $\mu$ 是其期望值，即